En Física, potencia es la cantidad de trabajo efectuado por unidad de tiempo. Esto es equivalente a la velocidad de cambio de energía en un sistema o al tiempo empleado en realizar un trabajo, según queda definido por:

Donde
- P es la potencia.
- W es la energía total o trabajo.
- t es el tiempo.
Potencia mecánica es el trabajo realizado por una máquina o una persona en un determinado intervalo de tiempo.
Potencia mecánica
La potencia mecánica es la potencia transmitida mediante la acción de fuerzas físicas de contacto o elementos mecánicos asociados como palancas, engranajes, etc. El caso más simple es el de una partícula libre sobre la que actúa una fuerza variable. De acuerdo con la dinámica clásica esta potencia viene dada por la variación de su energía cinética o trabajo realizado por unidad de tiempo:

Donde:
 , son la energía cinética y la masa del partícula, respectivamente
, son la energía cinética y la masa del partícula, respectivamente  son la fuerza resultante que actúa sobre la partícula y la velocidad de la partícula, respectivamente.
son la fuerza resultante que actúa sobre la partícula y la velocidad de la partícula, respectivamente.
En sistemas mecánicos más complejos con elementos rotativos sobre un eje constante y donde el momento de inercia permanece constante, la potencia mecánica puede relacionarse con el par motor, la velocidad angular siendo la potencia la variación de la energía cinética de rotación por unidad de tiempo:

Donde:
 , es el momento de inercia según eje de giro.
, es el momento de inercia según eje de giro.  , es la velocidad angular del eje.
, es la velocidad angular del eje. 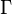 , es el par motor aplicado sobre dicho eje.
, es el par motor aplicado sobre dicho eje.
Si el movimiento rotativo puede darse según un eje variable o el momento de inercia es variable la expresión correcta es:

Donde:
 , son respectivamente la aceleración angular y el momento angular total del sistema.
, son respectivamente la aceleración angular y el momento angular total del sistema.
Esta última ecuación es análoga a la variación de potencia que se deriva de la ecuación del cohete donde al irse quemando combustible la masa no permanece constante
Potencia sonora
La potencia del sonido se puede considerar en función de la intensidad y la superficie:
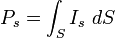
- Ps es la potencia realizada.
- Is es la intensidad sonora.
- dS es el elemento de superficie, sobre la que impacta la onda sonora.
Unidades de potencia
- Sistema métrico (SI), la más frecuente es el vatio (W) y sus múltiplos: 1000 W = 1 kW (kilovatio); 1 000 000 W = 1 MW (megavatio), aunque también pueden usarse combinaciones equivalentes como el voltiamperio.
- Sistema inglés, caballo de vapor o caballo de fuerza métrico (CV), cuya equivalencia es 1 kW = 1,359 CV
- Sistema técnico de unidades, caloría internacional por segundo (cal IT/s).
- Sistema cegesimal: ergio por segundo (erg/s)